ShipGen

The Basics

Below you can find the most upto date information on this project:

Ship Design and Machine Learning

Ship design is a years-long process that requires balancing complex design trade-offs to create a ship that is efficient and effective. Finding new ways to improve the ship design process can lead to significant cost savings in the time and effort required to design a ship and cost savings in the procurement and operation of a ship. Over 70% of the cost of a ship is embedded in the hull's design. By leveraging machine learning tools for data driven design, we aim to reduce the cost of ships, reduce greenhouse gas emissions, and improve the global supply chain with better ship hull design. This project looks at using diffusion models (DDPMs), a type of generative artificial intelligence, to generate parametric ship hull designs. DDPMs are great tools for ship design as they can be customized to generate designs with unique performance criteria without retraining. This customization comes from a process called guidance, where the gradients of pretrained neural networks are used to influence design generation. The ShipGen DDPM model uses 8 pretrained networks to generate ship hulls for improved feasiblity and performance from multiple objectives. This project page details the parametric design scheme for ship hulls, the dataset of ship hulls, and the ShipGen DDPM model.

Parametric Ship Hull Design

A parametric design scheme was created so that a single set of parameters can represent a large diversity of ship hull designs. This parametric scheme consists of 45 parameters that are used in a set of algebraic equations to define the surface of a hull. These 45 parameters define:

1) Principal Dimensions (7 parameters)

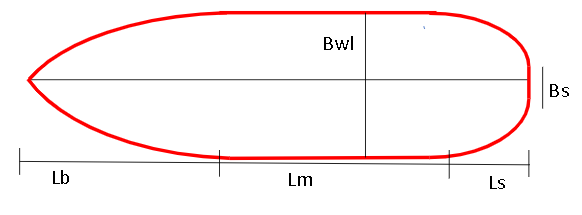
2) Midship Cross Section Geometry (4 parameters)

3) Bow and Stern Geometries (20 parameters)

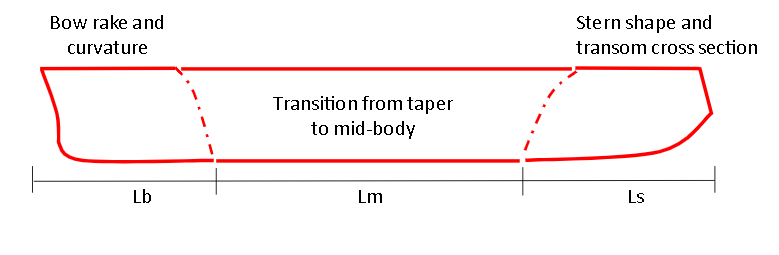
4) Bulbous Bow and Bulbous Stern Geometries (14 parameters)

In addition to these 45 parameters, a set of 49 algebraic constraints were defined to ensure that a given parameterized hull design is feasible. These 49 constraints efficiently check that a parameterized hull design will satisfy two criteria:

1) The hull is watertight
2) The hull is not self-intersecting

The algebraic design constraints are much faster at computing hull feasibility than constructing a mesh and checking these conditions by analyzing the mesh.
These 45 parameters can define most monohull designs and a much larger design space on a single set of parameters so that a machine learning tool can be trained to generalize the design process. Here are some examples of hulls reconstructed using this parametric design scheme:

A) Container Ship B) USS Zumwalt C) Fast Ferry D) Recreational Fishing Boat E) USS Freedom F) USS Nimitz G) Sailing Yacht H) Tug Boat I) USS Indianapolis J) X-Bow Ship K) Wigley Hull L) DTMB 5415

Dataset Creation.

The first step in our work was to create a dataset of ship hull designs. The ShipD Dataset comprises of 30,000 parametric ship hull designs. In addition to design parameters, the dataset also includes performance metrics, meshes, and images of each hull.

The performance measures of the hull include both geometric measures and measures of drag. There are ten geometric measures that are computerd at several draftmarks along each hull:

1) Displaced Volume
2) Surface Area
3) Waterplane Area
4) Area Moments of Intertia in Roll Direction
5) Area Moments of Intertia in Pitch Direction
6) Longitudinal Center of Flotation (Center of Waterplane Area)
7) Longitudinal Center of Buoyancy (Center of Displaced Volume)
8) Vertical Center of Buoyancy (Center of Displaced Volume)
9) Waterline length
10) Height of draft measurement

Two additional geometric measures are computed using the full geometry of each hull:

11) Gaussian Curvature
12) Largest Box that can be vertically lowered into the hull. (Called MaxBox)

Additionally, there are 32 Wave drag coefficients across 8 speeds and 4 draft marks using Michell integral, 5 images of each hull, and surface meshes

As the hulls in the ShipD dataset are randomly sampled from the design space, they do not necessarily look like realistic ship hull designs. The video below showcases some of the unique hull geometries found in the dataset.

Most of the ShipD hulls in the dataset are relatively low performing. They have high drag, low volume, and complicated double curvature geometries that lead to hull shapes that do not look like realistic hulls.

The real value of these hulls is data they provide. With these 30,000 hulls, there is sufficient information to learn how the 45 design parameters affect the many performance measures found in the dataset. The next section applies a diffusion model to this dataset to learn the relationship between the design parameters and the performance measures, allowing the model to generate high performing hull designs.

Guided Diffusion for High Performing Ship Hull Generation

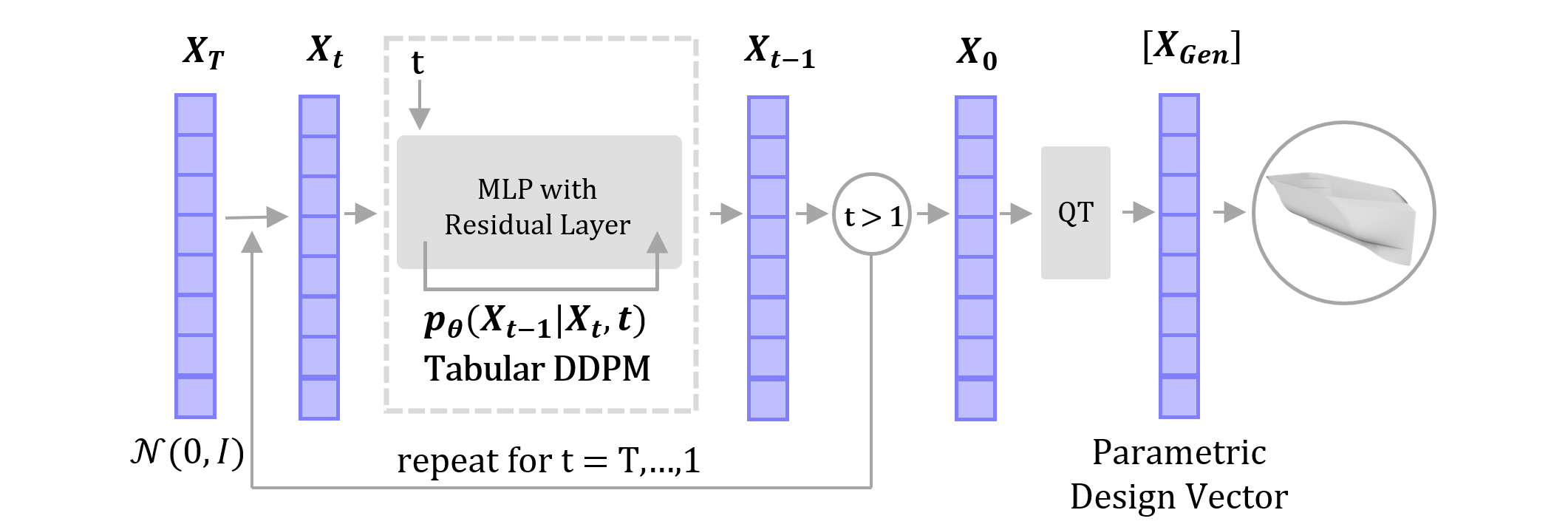
The ShipD dataset provides a large amount of information to create a data driven approach to hull design. This work leverages a diffusion model (DPPM), a type of generative artificial intelligence, to generate ship hull designs. DDPMs iteratively modify a noisy data vector over a number of specified steps, transforming random data to mirror the statistics of training data. To train a DDPM model, partially noise a parametric design vector with a time embedding and predict a noise vecotor with the DDPM. The mean squared loss between the predicted noise vector and the initial noise vector backpropagates through the DDPM to update the model weights. Repeat this process in batches with random time embeddings and design vectors to train the DDPM.

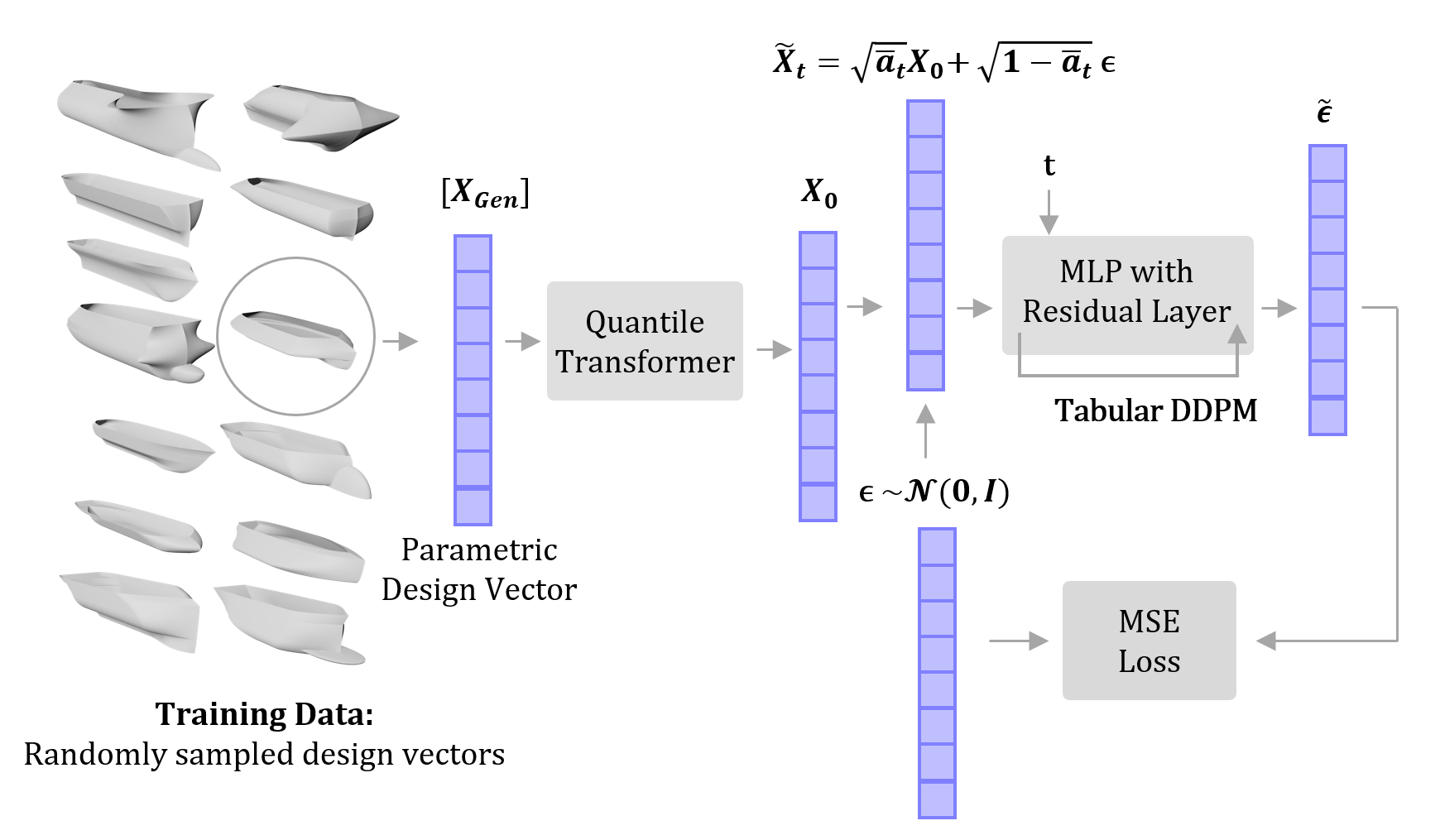
With a trained DDPM, the model can be used to denoise a vector over many timesteps to create a parametric ship hull design. Samples created with a standard DDPM will resemble the hull designs found in the training dataset.

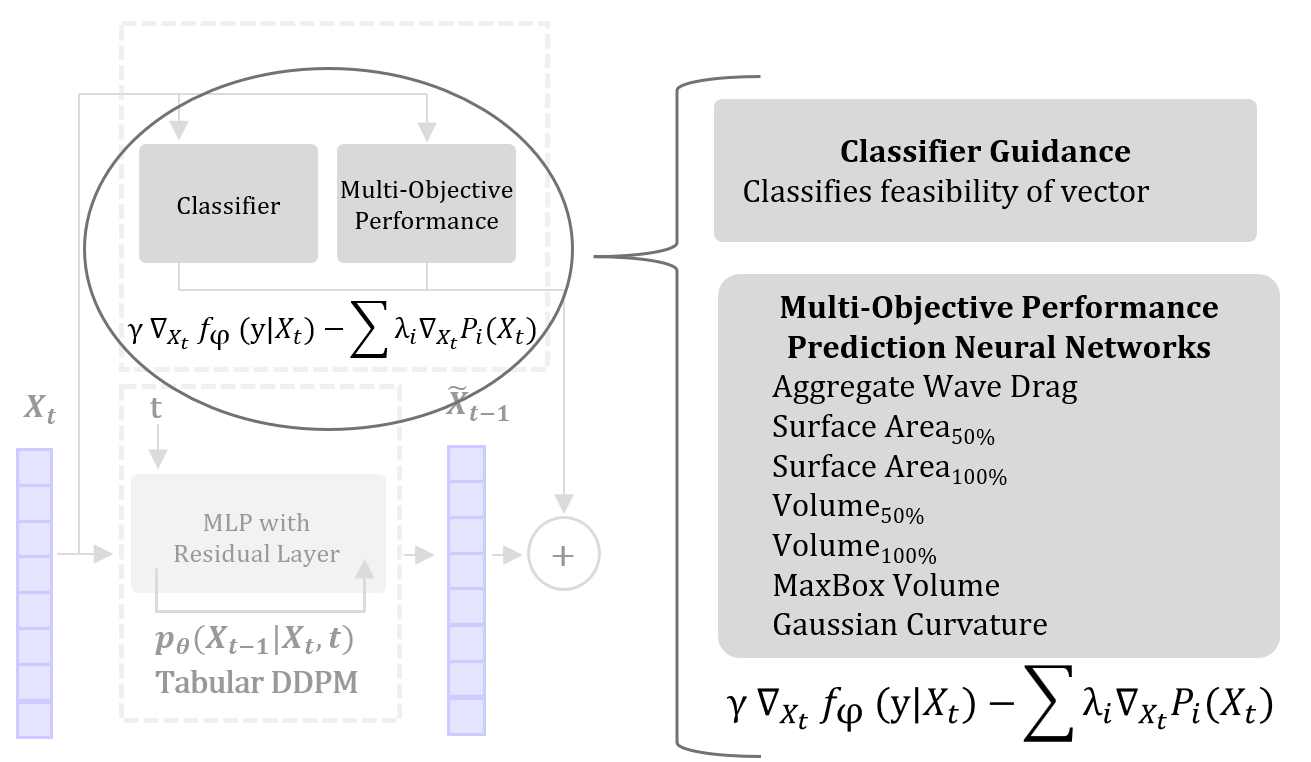
One major adavantage of DDPMs over other types of generative models is that they can be customized to generate designs with unique performance criteria without retraining. This is done through a process called guidance, where the gradients of pretrained neural networks are used to influence design generation. The ShipGen DDPM model leverages guidance from 8 pretrained neural networks to create designs with improved performance and feasibility.

1) Design Feasibility
2) Drag
3) Surface Area of the bottom 50% of the hull
4) Surace Area of the whole hull
5) Volume of the bottom 50% of the hull
6) Volume of the whole hull
7) MaxBox Guidance
8) Gaussian Curvature

Samples generated with a guided DDPM will yield high performing hull designs.

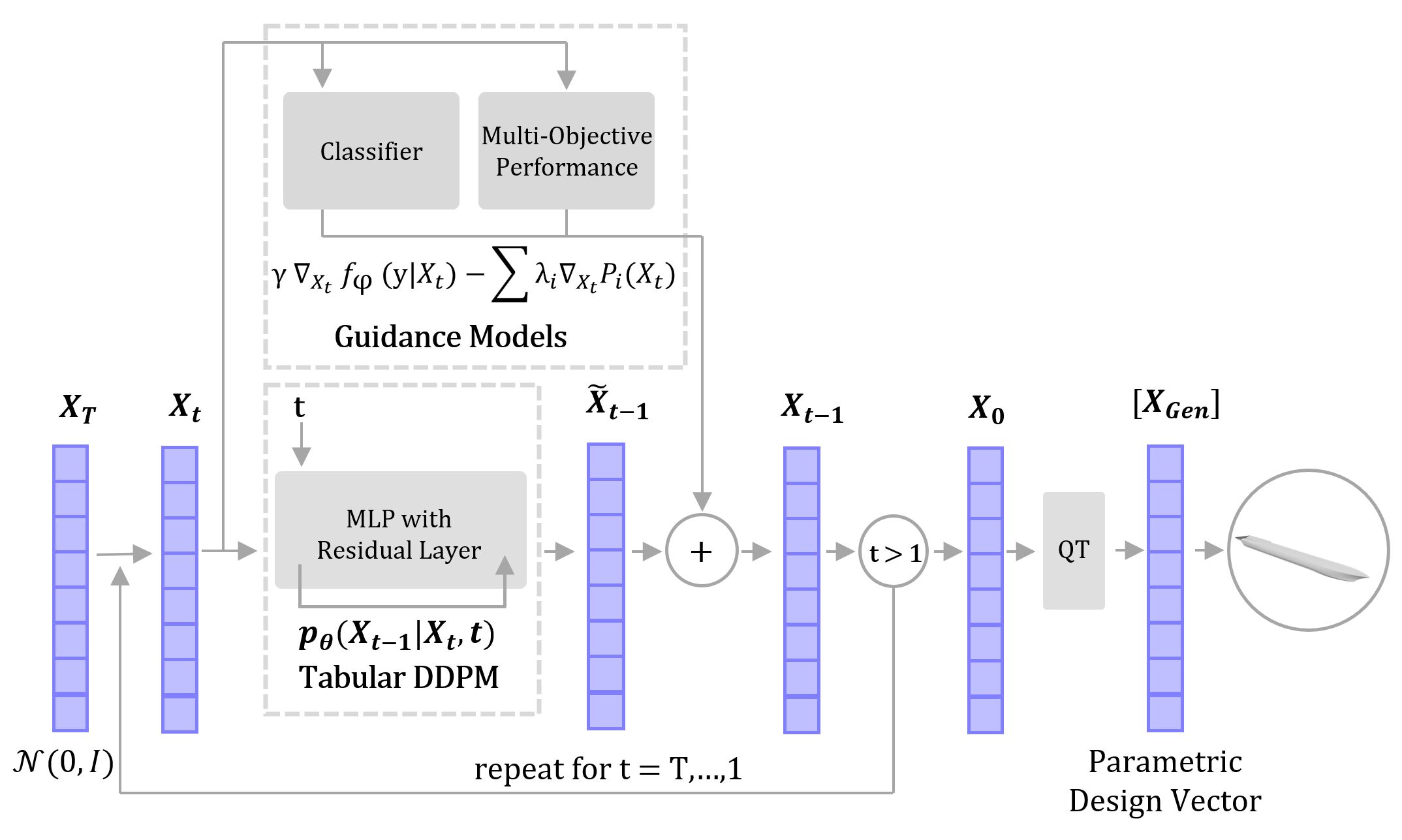
Ship hulls generated with this tabular guided diffusion model saw a 91.4% decrease in drag coefficient and 47x relative increase in total displaced volume compared to hulls belonging in the ShipD dataset. In addition, these hulls look more like realistic ships than the hulls belonging to the original ShipD Dataset. For example, these hulls are more slender and have streamlined bodies seen in traditional hull designs. The video below showcases some of these generated hull designs.

Citations

Citations

ACKNOWLEDGEMENT

The authors acknowledge the MIT supercloud for providing computational resources for some of the work performed in this project. We also want to thank the United States' Department of Defense for supporting our work through the National Defense Science and Engineering Graduate Fellowship (NDSEG) Program.