C-ShipGen

The Basics

Below you can find the most up-to-date information on this project:

Introduction

C-ShipGen is a conditional guided diffusion model for parametric ship hull design. This model allows users to generate hulls specifically tailored to desired principal characteristics. A designer provides the length, beam, draft, depth, block coefficient, and design speed of a hull. C-ShipGen then generates a set of low drag hulls that meet these dimensional specifications. The following sections detail C-ShipGen's training, sampling, and evaluation processes.

Training C-ShipGen

C-ShipGen is trained on 82,168 hull designs. These designs are comprised of 30,000 hulls from the original ShipD dataset and 52,168 hulls generated with a ShipGen, a diffusion model that considers 7 performance metrics when generating the hull. Below are some examples of the dataset hulls.

First are the original ShipD hulls. These hulls are randomly sampled from the design space and do not necessarily look like realistic ship hulls.

Next are the hulls generated with using a guided diffusion model trained on the original ShipD dataset. These hulls are high performing and look more like realistic ship hulls."

The dataset contains the following information for each hull in the dataset:
1) Design Parameters
2) Beam Overall
3) Displaced Volume measured across 100 draft marks
4) Wetted Surface Area measured across 100 draft marks
5) Waterline length measured across 100 draft marks
6) Wave Drag measured across 8 speeds and 4 draft marks (32 total)

With these measurements, regression models were trained to predict the performance metrics of a set of design parameters given a the draft, length overall, and the desired speed. Below is the training algorithm for the total resistance coefficient regression model:

The regression model is trained to consider both the wave making resistance and the skin friction resistance on a hull for a given draft, speed, and length overall. This is done so that the model can be used to predict the total resistance coefficient of a hull across the large length scales seen in ship hulls. This model is trained with hulls scaled from 3.5 to 450 meters in length.

After the regression models were trained, the Conditional Diffusion Model was trained. C-ShipGen is a conditional denoising diffusion probabilistic model. To train a diffusion model, random noise is iteratively added to the design parameters of a hull so that the model can learn to generate information that is statistically similar to the training data. As this model is trained on hull design information, C-ShipGen will generate information that is statistically similar to the hull designs in the training dataset.

The conditional aspect of the diffusion model means that a user can provide extra information to the model during sampling. This way, the diffusion model will generate hull designs that are statistically similar to hulls within the dataset that have the same conditioning label. For C-ShipGen, the principal characteristics of a hull is the conditioning information. Therefore, C-ShipGen will generate designs that have the principal characteristics provided by the user during sampling. Below is the training algorithm for C-ShipGen:

During training, no performance information is provided to the model. Only hull design information is used to train C-ShipGen. The principal characteristics of each hull is fed to C-ShipGen as a conditioning vector separate from the design parameters. The conditioning vector then acts as a label for the hull design information. In each step in the loop, a timestep and a noise vector are randomly sampled to train the diffusion model to iteratively denoise the noisy design parameters. The training algorithm is better visualized in the image below:

Sampling C-ShipGen

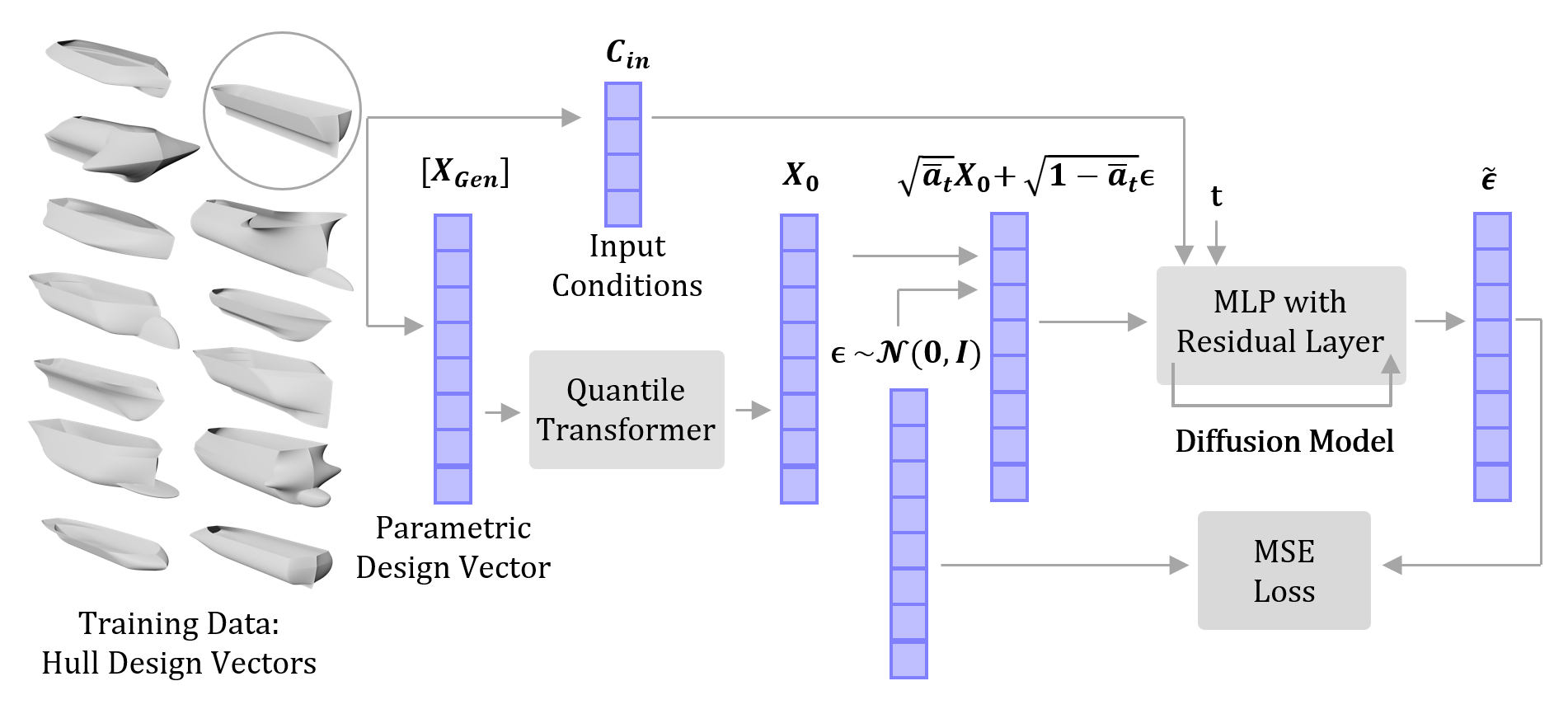
After training, C-ShipGen generates parametric hull designs based on a set of principal characteristics of a desired hull. At each denoising step, gradients from the volume prediction model and the drag prediction model are used to guide the diffusion model. The volume guidance is structured to further aid in satisfying the specified block coefficient. The drag guidance is structured to minimize the total resistance coefficient of the hull. The algorithm for sampling a hull design is as follows:

The image below better illustrates the sampling process, showcasing how the input conditioning feeds information to the diffusion model and to the guidance algorithms at every denoising step.

Sample Evaluation

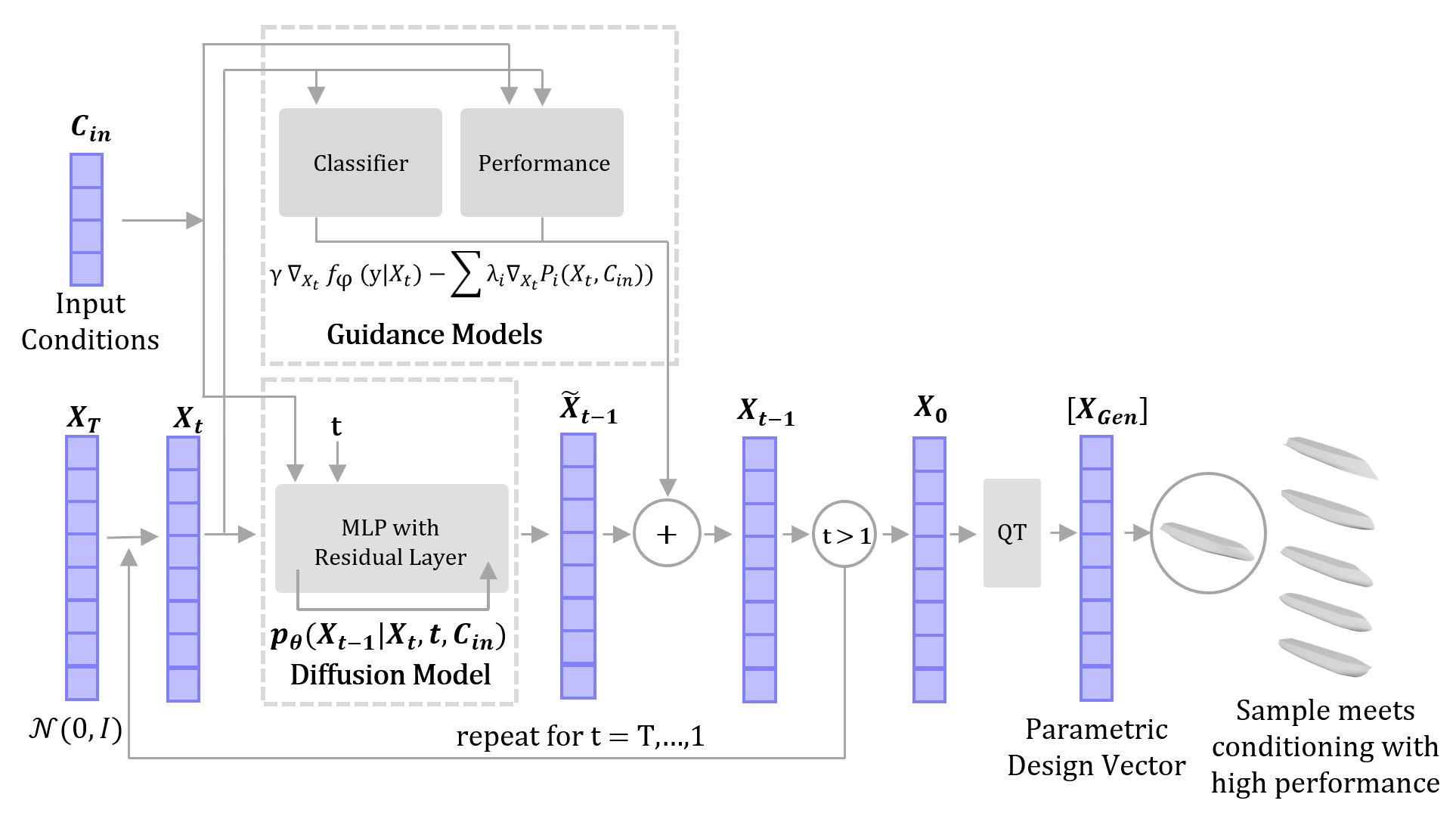
In the study, a few ship classes were identified to evaluate the performance of C-ShipGen. For each set of principal characteristics, 512 hulls were generated with C-ShipGen, and 100 hulls were generated using NSGA-II. The NSGA-II hulls were generated with the same principal characteristics as the C-ShipGen hulls, using the total resistance regression model as the objective function in the optimization. C-ShipGen can generate a few hundred hulls in a matter of seconds, while the 100 NSGA-II generated hulls required approximately one hour of computation to create. Here examples of some of the C-ShipGen hulls.

These hulls have the principal characteristics requested by the user; however, they do not necessarily look like real hulls that belong to the intended ship class. This is because the hulls were generated to meet the dimensional properties of the conditioning and have reduced drag. The design of these hulls is affected by the distribution of parametric hull design vectors in the dataset. In real ships, other performance characteristics, such as stability, seakeeping, and manufacturability also strongly affect the design of a hull.

The C-ShipGen generated hulls and the NSGA-II generated hulls were simulated for drag using the Michell Integral. The figure below shows the comparison of the regression prediction versus the simulated total resistance for the supercarrier class hulls.

In this test case, the regression model maintains a high degree of accuracy to the simulation among C-ShipGen generated hulls. This is because the regression model and the diffusion model were trained on the same dataset of hulls. Since C-ShipGen will generate hulls with statistical similarity to the original training data, the generated hulls will have highly accurate regression predictions. The NSGA-II generated hulls, however, do not have the same regression accuracy. This is because NSGA-II exploited the regression model, finding a minimum in the regression model where there is not a true local minimum. This pattern is similarly true for the other ship classes.

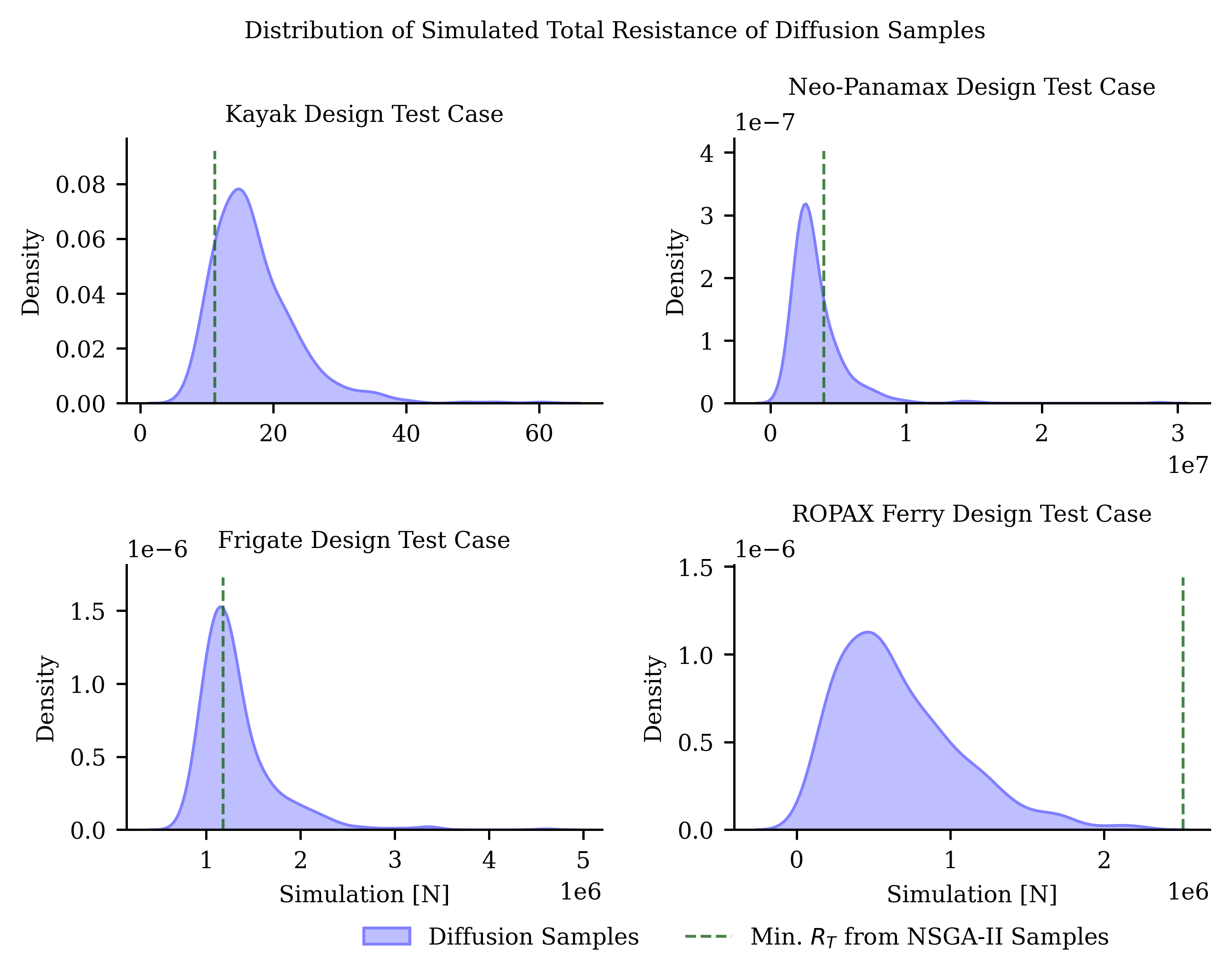
Another way to compare C-ShipGen to NSGA-II is to look at the distribution of total drag among hulls generated by each method. The figure below shows the distribution of total drag among hulls generated by C-ShipGen for the supercarrier class. This plot also has a line indicating the minimum drag found on a hull using NSGA-II to generate the same class of hulls.

The plot suggests that C-ShipGen will generated hulls with a lower total drag than NSGA-II approximately 15% of the time while still maintaining the principal characteristics of the hull. Since the C-ShipGen hulls will have highly accurate predictions of total resistance, the generated hulls can be quickly sorted to identify the hulls with the lowest drag. This is the major benefit of using C-ShipGen to create a set of candidate hull designs for future analysis.

For the other classes, C-ShipGen generated hulls with lower drag than NSGA-II approximately 15-100% of the time depending on the intended principal characteristics.

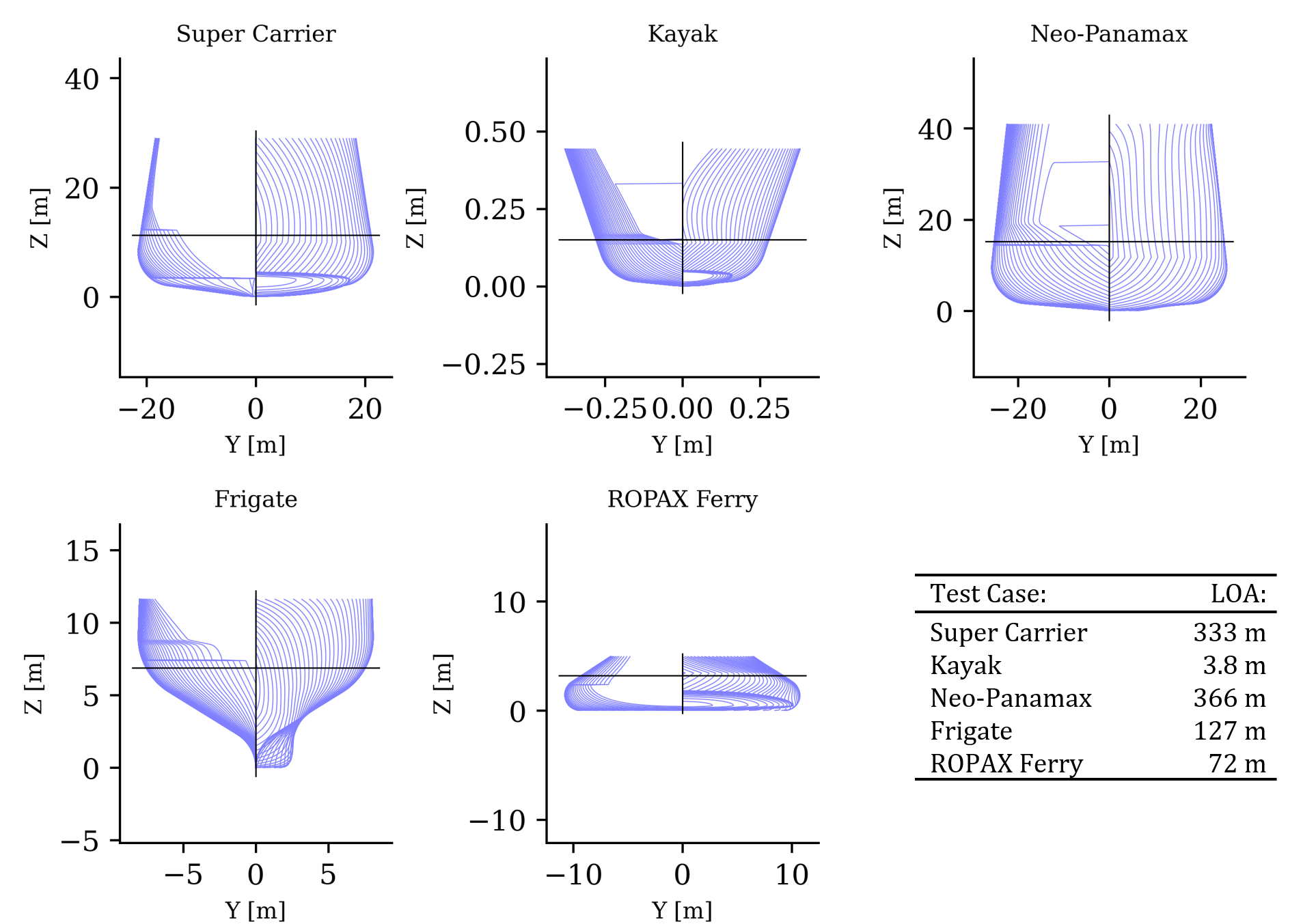
Here are a few lines plans of hulls generated by C-ShipGen. These hulls were the hulls with the minimum total drag among the 512 samples in each class.

While C-ShipGen provides a great way to rapid generate many concept hull designs, further evaluation is needed by a team of humans to determine the feasibility and safety of using an AI generated hull in a real world ship design.

ACKNOWLEDGEMENT

The authors acknowledge the MIT supercloud for providing computational resources for some of the work performed in this project. We also want to thank the United States' Department of Defense for supporting our work through the National Defense Science and Engineering Graduate Fellowship (NDSEG) Program.